我们知道，在国际象棋中，皇后可以在行、列和对角线上行走。那么考虑一下：如何在一个N * N 的棋盘上放置 N个皇后，使得每行、每列和每条对角线上不存在2个或2个以上的皇后。这实际上就是经典的N-皇后问题。N-皇后问题是人工智能领域中一个经典的组合问题，在包括VLSI和交通控制等问题上具有广泛的应用。图1 给出了包含4个皇后的4-皇后问题的例子。图1 (a)给出了一个违反了约束的解的例子。可以发现，每一行、每一列上均只有1个皇后，但是第1列和第2列的两个皇后在正对角线方向上违反了约束。而图1 (b)给出了一个合法解，在每一行、每一列均只有1个皇后，而且在正对角线、负对角线方向上最多只有一个皇后。

N-皇后问题是我们在数据结构和算法类的课程上经常遇到的一个问题，它的经典求解方法是采用回溯的方法，可以产生所有的可行解，但是实际上运行时间非常长，能够解决的问题规模相对非常小。有没有一种方法，可以在极短的时间内求解上百万个皇后的N-皇后问题？答案是可以，用局部搜索！Rok Sosic和Jun Gu （顾钧）在20余年前提出的系列快速局部搜索算法可以在极短的时间内，求解百万量级的N-皇后问题。

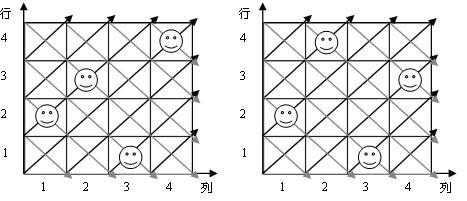
(a)违反约束的解                  (b)一个合法解

                         并在其邻域中寻找更好的解X'。在算法步骤（3），当邻域中有多个更好解时，局部搜索可以有不同的实现方法，比较常见的是选择邻域中遇到第一个更好解作为当前解，或者选择邻域中最好的更好解。

算法2 Local Search
输入: 实例
输出: 解X* 
Begin
(1) 按照某种方法生成一个初始解X
(2) X* = X
(3) While X* 的邻域中有更好的解 X'
         X* = X' 
    Endwhile
(4) 输出 X*
End

下面针对局部搜索算法的两个基本操作（初始解生成及邻域定义）进一步讨论。

（1）初始解生成

在局部搜索算法中，初始解是搜索的起点。常见的初始解生成方法包括随机解或者采用某种构造算法来获得初始解。比如在旅行商问题中，可以采用贪心法来构造初始解：从某个城市出发，每次都挑选最近的未访问过的城市，并将其标注为已访问，重复该过程知道完整的城市环路构造成功。

（2）解的邻域定义
解的邻域定义是局部搜索算法中的关键，也是需要算法设计人员精心研究的范畴。邻域的规模大小决定了局部搜索的收敛速度：当邻域规模较小时，局部搜索很快就可以达到收敛状态（即求得局部最优解）；当邻域规模较大时，局部搜索在邻域中的遍历时间将显著增长。极端的情形下，当邻域选择为整个解空间且采用的是邻域中最好解时，局部搜索就退化为一般的全局优化了。

参考文献
[1]Sosic, R.;   Gu, J. A polynomial time algorithm for the N-Queens problem. ACM SIGART Bulletin, 1(3).
[2]Sosic, R.;   Gu, J. Fast search algorithms for the n-queens problem. IEEE Transactions on Systems, Man and Cybernetics, 1991, 21(6): 1572 - 1576.
[3]Sosic, R.;   Gu, J. 3,000,000 Queens in less than one minute. ACM SIGART Bulletin, 1991, 2(2).
[4]Sosic, R.;   Gu, J. Efficient local search with conflict minimization: a case study of the n-queens problem. IEEE Transactions on Knowledge and Data Engineering, 1994, 6(5):661 - 668