杜宗亮，1987年生，大连理工大学副教授，博士生导师，工业装备结构分析优化与CAE软件全国重点实验室固定成员，入选大连市高端人才、大连理工大学“星海青千引进计划”。已在固体力学和计算力学领域的著名期刊（JMPS、CMAME等）发表学术论文70余篇，谷歌学术引用2000余次。曾获得亚洲结构与多学科优化学会青年科学家奖（ACSMO Young Scientist Award），大连市青年科技之星等奖励奖项。主持国家级重点项目课题、国家自然科学基金（面上、青年项目）、辽宁省应用基础研究计划（青年项目）等。现任辽宁省力学学会理事、《力学进展》和《应用力学学报》青年编委，《Frontiers in Physics》associate editor.

课题组新闻

2024-08-16  祝贺与同济大学合作的论文“A new seismic metamaterial design with ultra-wide low-frequency wave suppression band utilizing negative Poisson's ratio material”被《Engineering Structures》接受

2024-08-02  祝贺与韩国蔚山科技大学合作的论文“Explicit topology optimization of large deforming hyperelastic composite structures”被《Structural and Multidisciplinary Optimization》接受

2024-06-20  祝贺贾宜播同学的论文“Explicit design optimization of air rudders for maximizing stiffness and fundamental frequency”被《Thin-Walled Structures》接受

2024-06-18  祝贺李世东同学硕士毕业，并将到吉林江机特种工业有限公司工作；祝贺马新宇同学获得大连理工大学优秀硕士学位论文，并将到清华大学深造；祝贺徐志昂同学获得大连理工大学优秀本科毕业论文

2024-04-29  祝贺任晓强同学的论文“Finite deformation analysis of bi-modulus thermoelastic structures and its application in wrinkling prediction of membranes”被《Computer Methods in Applied Mechanics and Engineering》接受

2024-04-09  祝贺丁相贵同学的论文“Optimal design of fast adiabatic topological pumping in modulated lattices”被《Applied Physics Letters》接受

2024-04-01  祝贺贾宜播同学获得2024年全国固体力学学术会议“博士生论坛-优秀报告奖”

2024-01-11  祝贺郭云航同学通过题为《基于经典本构模型及数据驱动本构模型的三维非线性连续体结构显式拓扑优化研究》博士学位论文答辩，并将到航天科工三院301所工作

2023-11-30  祝贺边汤淮同学的论文“Inverse design of mechanical metamaterial achieving a prescribed constitutive curve”被《Theoretical and Applied Mechanics Letters》接受

2023-11-02  祝贺郭云航同学的论文“Structural topology optimization of three-dimensional multi-material composite structures with finite deformation”被《Composite Structures》接受

2023-10-24  祝贺程旭兵同学的报告“基于相容边界条件的力学隐身拓扑优化设计新范式”获得第一届波动力学前沿与应用研讨会的最佳报告奖，相关论文发表于《Extreme Mechanics Letters》

2023-09-08  祝贺黄孟成同学的论文“A sequential linear programming (SLP) approach for uncertainty analysis-based data-driven computational mechanics”被《Computational Mechanics》接受

2023-09-01  祝贺骆嘉晨同学通过题为《拓扑绝缘体的拓扑优化研究》博士学位论文答辩，并将去波士顿大学从事博士后研究

2023-09-01  祝贺郝文宇同学的论文“Artificial intelligence-enhanced bioinspiration: Design of optimized mechanical lattices beyond deep-sea sponges”被选为《Extreme Mechanics Letters》封面文章

2023-07-26  杜宗亮老师受聘《Frontiers in Physics》副编辑

招收硕士研究生专业

固体力学、计算力学、工程力学

欢迎力学、物理、机械、计算机、数学等相关方向同学加入课题组共同奋斗！        

主讲课程

Mechanics of Plates and Shells  本科生  英语授课  48学时 

科研项目

·  国家级重点项目课题，基于数据驱动的超结构设计，2022-2026，负责

·  国家自然科学基金面上项目，考虑热力耦合和有限变形的薄膜结构高效褶皱分析与优化设计，2024-2027，负责

·  国家自然科学基金青年项目，基于结构拓扑优化的最优力学拓扑绝缘体设计，2021-2023，负责

·  辽宁省应用基础研究计划（青年项目），显式结构拓扑优化理论算法与自主可控软件研发，2023-2025，负责

·  航空科学基金，基于显式拓扑优化框架的智能柔性结构设计理论与方法，2020-2022，负责

·  大连市高层次人才创新支持计划（青年科技之星），三维力学拓扑绝缘体优化设计及波动调控，2021-2022，负责

·  技术开发项目，兆瓦级海上风机主承载部件减重拓扑优化设计，2022-2024，负责

·  技术开发项目，空气舵快速设计优化软件，2020-2022，负责

·  国家重点研发计划，结构拓扑优化核心算法研究与集成，2020-2023，参与

研究兴趣及近五年成果

当前研究兴趣为结构拓扑优化、拓扑力学、基于机器学习的先进材料/结构设计、非光滑力学等。近五年代表性研究成果如下：

²  结构拓扑优化

针对非线性显式结构拓扑优化、大规模结构拓扑优化问题的高效算法、基于数据驱动计算力学的结构拓扑优化设计、考虑可制造性的多尺度结构拓扑优化问题等开展研究，取得了系列成果。

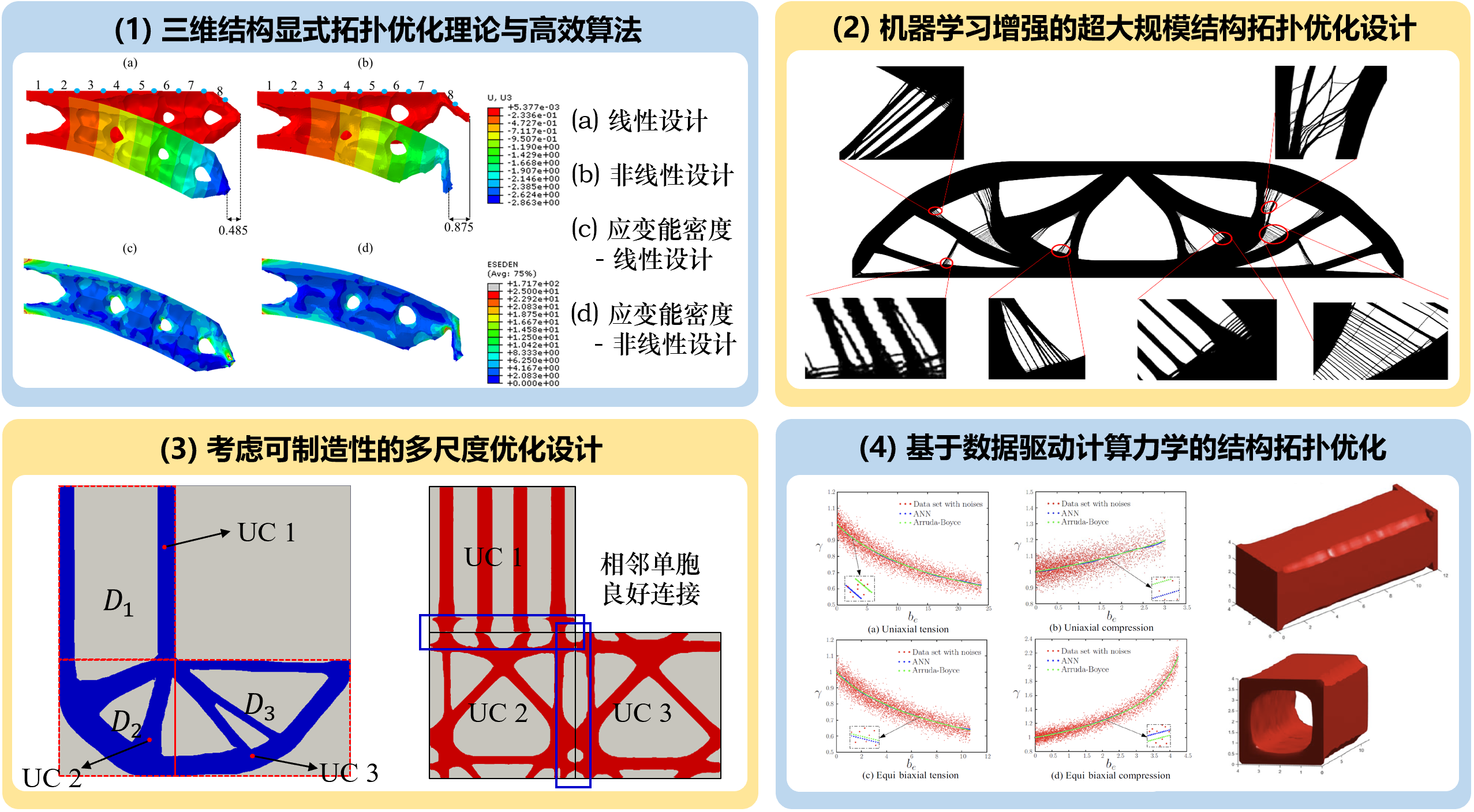
相关代表性论文（*为通讯作者）：

–   Y. Guo, Z. Du*, L. Wang, W. Meng, T. Zhang, R. Su, D. Yang, S. Tang*, X. Guo*. Data-driven topology optimization (DDTO) for three-dimensional continuum structures. Struct Multidisc Optim, 66(2023), 104.（结构与多学科优化旗舰期刊）

–   Z. Du, T. Cui, C. Liu, W. Zhang, Y. Guo, X. Guo*. An efficient and easy-to-extend Matlab code of the Moving Morphable Component (MMC) method for three-dimensional topology optimization. Struct Multidisc Optim, 65(2022), 158.（结构与多学科优化旗舰期刊）

–   C. Liu, Z. Du*, Y. Zhu, W. Zhang, X. Zhang, X. Guo*. Optimal design of shell-graded-infill structures by a hybrid MMC-MMV approach. Comput Methods Appl Mech Engrg, 369(2020), 113187.（计算力学旗舰期刊）

–   R. Xue, C. Liu, W. Zhang, Y. Zhu, S. Tang, Z. Du*, X. Guo*. Explicit structural topology optimization under finite deformation via Moving Morphable Void (MMV) approach. Comput Methods Appl Mech Engrg, 344(2019), 798-818.（计算力学旗舰期刊）

²  拓扑力学

提出了最优力学拓扑绝缘体的数学模型，建立了基于“理性能带工程”的最优拓扑绝缘体优化设计列式；在力学系统应用并推广了对称指标理论，发展了多类型、多功能拓扑材料的系统性设计理论与算法。

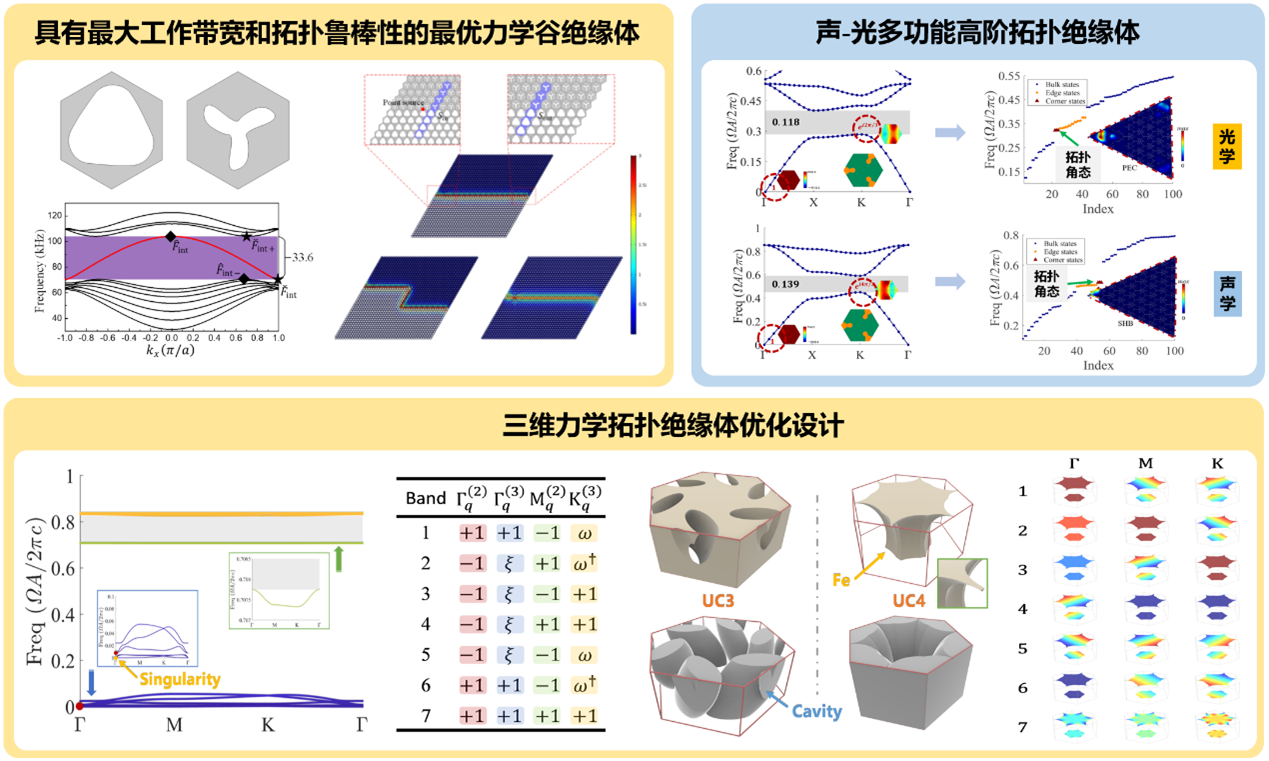
相关代表性论文（*为通讯作者）：

–   J. Luo, Z. Du*, H. Chen, X. Ding, C. Liu, W. Zhang, X. Guo*. Efficient design of helical higher-order topological insulators in 3D elastic medium. J Mech Phys Solids, 176(2023), 105325.（固体力学旗舰期刊，入选该期Highlights论文）

–   J. Luo, Z. Du*, Y. Guo, C. Liu, W. Zhang, X. Guo*. Multi-class, multi-functional design of photonic topological insulators by rational symmetry-indicators engineering. Nanophotonics, 10(2021), 4523-4531.

–   J. Luo, Z. Du*, C. Liu*, Y. Mei, W. Zhang, X. Guo. Moving morphable components-based inverse design formulation for quantum valley/spin Hall insulators. Extreme Mech Lett, 45(2021), 101276.（入选该期Highlights论文）

–   Z. Du, H. Chen, G. Huang*. Optimal quantum valley Hall insulators by rationally engineering Berry curvature and band structure. J Mech Phys Solids, 135(2020), 103784.（固体力学旗舰期刊）

²  基于机器学习的先进材料/结构设计

发展了人工智能增强的仿生设计方法，相比文献中深海海绵微结构抗屈曲性能提升了40%；结合多任务学习，实现了拓扑绝缘体高效优化设计，相比模型分析的拓扑优化算法效率提升3-4个数量级。

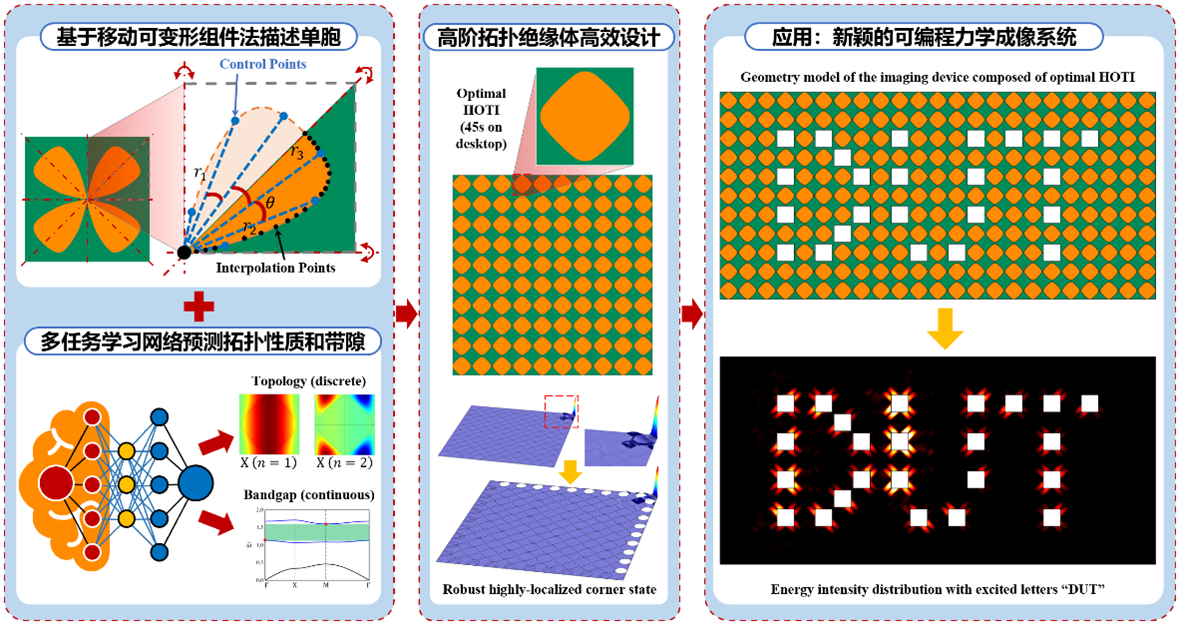
相关代表性论文（*为通讯作者）：

–   Z. Du, W. Hao, X. Chen, X. Hou, W. Huo, C. Liu, W. Zhang, T. Cui*, X. Guo*. Artificial intelligence-enhanced bioinspiration: design of optimized mechanical lattices beyond deep-sea sponges. Extreme Mech Lett, 62(2023), 102033.（入选该期Highlights论文、期刊封面）

–   Z. Du*, J. Luo, Z. Xu, Z. Jiang, X. Ding, T. Cui, X. Guo*. Higher-order topological insulators by ML-enhanced topology optimization. Int J Mech Sci, 255(2023), 108441.

–   Z. Du, X. Ding, H. Chen, C. Liu, W. Zhang, J. Luo*, X. Guo*. Optimal design of topological waveguides by machine learning. Front Mater, 9(2022), 1075073.

²  非光滑力学

针对拉压不同模量弹性系统，建立了系列变分原理和复合材料性质界限分析理论；发展了高效数值分析算法及结构拓扑优化理论；建立了拉压响应不同超弹性材料的有限变形力学分析模型，得到了系列封闭解析解。

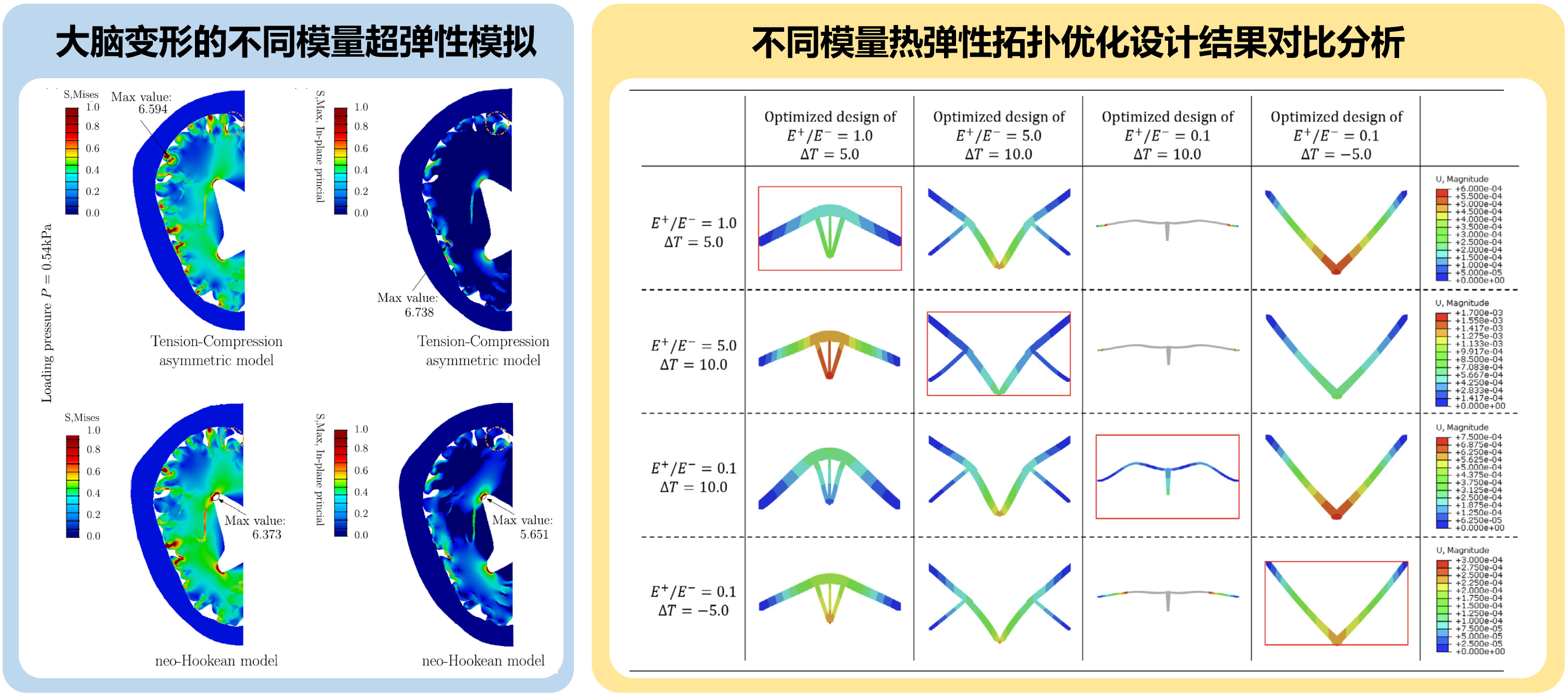
相关代表性论文（*为通讯作者）：

–   Z. Du, Y. Jia, H. Chung*, Y. Zhang, Y. Li, H. Zhou, X. Guo*. Analysis and optimization of thermoelastic structures with tension–compression asymmetry. Int J Solids Struct, 254(2022), 111897.（入选该期Highlights论文）

–   Z. Du, G. Zhang, T. Guo, S. Tang*, X. Guo*. Tension-compression asymmetry at finite strains: A theoretical model and exact solutions. J Mech Phys Solids, 143(2020), 104084.（固体力学旗舰期刊）

–   Z. Du, W. Zhang, Y. Zhang, R. Xue, X. Guo*. Structural topology optimization involving bi-modulus materials with asymmetric properties in tension and compression. Comput Mech, 63(2019), 335-363.

²  代表性工程应用

将设计算法与软件工具应用于我国新一代航空航天装备、大兆瓦级海上风机等重点型号的研发，与航天科技一院、科工四院、中航工业611所、东方风电等公司保持了密切合作关系；可为学生提供到相关企业的实习机会。